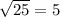Question

A certain circle can be represented by the following equation. x^2+y^2+18x+14y+105=0 What is the center of the circle? What is the radius of the circle?

Answer 1

See below.

Explanation:

Recall the equation for a circle:

`(x-h)^2+(y-k)^2=r^2`, where (h,k) is the center and r is the radius.

We need to turn the given equation into the above format. We do this by completing the square.

First, group them:

`(x^2+18x)+(y^2+14y)=-105`

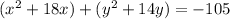
For the first section, complete the square for
`x^2+18x`:

`x^2+18x+81-81`

`(x+9)^2-81`

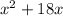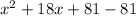
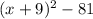
Do the same for the second:

`y^2+14y`

`y^2+14y+49-49`

`(y+7)^2-49`

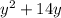
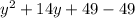
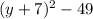
All together:

`((x+9)^2-81)+((y+7)^2-49)=-105`

`(x+9)^2+(y+7)^2-130=-105`

`(x+9)^2+(y+7)^2=25`

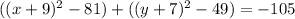
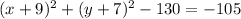
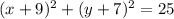
The center is (-9,-7).

The radius is
`√(25)=5`