Answer:
a. 95.4
b. UCL = 96.07
LCL = 94.73
c. Process is in control
Explanation:
a. The computation of estimate mean is shown below:-
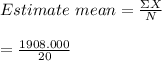
= 95.4
b. The computation of Upper Control Limit (UCL) and the Lower Control Limit (LCL) for the manufacturing process is shown below:-
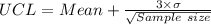
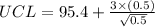
= 95.4 + 0.67082
= 96.07
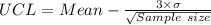
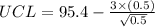
= 95.4 - 0.67082
= 94.73
c. The explanation is shown below:-
From the above calculation we can see that the sample lies between LCL AND UCL that is (94.73 ,96.07) ,
The Process is in control