Question:
Write out the first three terms and the last term. Then use the formula for the sum of the first n terms of an arithmetic sequence to find the indicated sum.
30
∑ (−3i+5)
i=1
Answer:
The first three terms are : 2, -1 and -4
The last term is: -85
The sum of the sequence is: -1245
Explanation:
Given;
==================================
30
∑ (−3i+5) -------------------(i)
i=1
==================================
Where the ith term aₙ is given by;
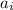 =
=
 -------------------(ii)
-------------------(ii)
(a) Therefore, to get the first three terms (
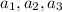 ), we substitute i=1,2 and 3 into equation (ii) as follows;
), we substitute i=1,2 and 3 into equation (ii) as follows;
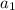 =
=
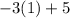 = 2
= 2

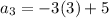

Since the sum expression in equation (i) goes from i=1 to 30, then the last term of the sequence is when i = 30. This is given by;
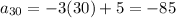
(b) The sum
 of an arithmetic sequence is given by;
of an arithmetic sequence is given by;
![s_n = (n)/(2)[a_1 + a_n]](https://img.qammunity.org/2021/formulas/mathematics/college/u7h0rsucbxl3qv9u9f6y70reqju2n5r1m5.png) -----------------(iii)
-----------------(iii)
Where;
n = number of terms in the sequence = 30
 = first term = 2
= first term = 2
 = last term = -85
= last term = -85
Substitute the corresponding values of n,
 and
and
 into equation (iii) as follows;
into equation (iii) as follows;
![s_n = (30)/(2)[2 + (-85)]](https://img.qammunity.org/2021/formulas/mathematics/college/c807ptneefhyske32j3dg44eu4ck4t73g5.png)
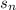 = 15[-83]
= 15[-83]
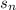 = -1245
= -1245