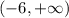Question

Consider the function below. (If an answer does not exist, enter DNE.) g(x) = 190 + 8x3 + x4 (a) Find the interval of increase. (Enter your answer using interval notation.)

Answer 1

The interval of increase of g(x) is
`(-6,+\infty)`.

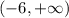Explanation:

The interval of increase occurs when first derivative of given function brings positive values. Let be
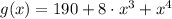`g(x) = 190 + 8 \cdot x^(3) + x^(4)`, the first derivative of the function is:

`g'(x) = 24 \cdot x ^(2) + 4\cdot x^(3)`

`g'(x) = 4 \cdot x^(2)\cdot (6+x)`

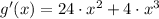
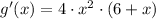
The following condition must be met to define the interval of increase:

`4\cdot x^(2) \cdot (x+6) > 0`

The first term is always position due to the quadratic form, the second one is a first order polynomial and it is known that positive value is a product of two positive or negative values. Then, the second form must satisfy this:

`x + 6 > 0`

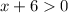
The solution to this inequation is:

`x > - 6`

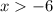
Now, the solution to this expression in interval notation is:
`(-6,+\infty)`