Question

use the figure and given information below. Show the calculations that lead to your results. Given: Polygon ROTFL ~ Polygon SUBAG Perimeter of ROTFL is 52. a) Find m∠G. (1 pt) b) Find AG. (2 pts) c) Find the perimeter of Polygon SUBAG. (2 pts)

Answer 1

a)
`\angle G = 125^\circ`

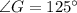
b) AG = 15 units

c) Perimeter of polygon SUBAG = 78 units

Explanation:

Given:

Polygon ROTFL ~ Polygon SUBAG

Similar polygons mean they have similar angles and the ratio of corresponding sides and ratio of their perimeter are equal.

Part A:

Given that

`m\angle R = 100^\circ\\m\angle O = 120^\circ\\m\angle T = 75^\circ\\M\angle L = 60^\circ`

`m\angle L+M\angle L = 180^\circ\\\Rightarrow m\angle L=180-60=120^\circ`

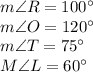
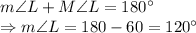
Sum of all interior angles of a pentagon is
`540^\circ`

`m\angle R+m\angle O+m\angle T+m\angle F+m\angle L=540^\circ\\\Rightarrow 100+120+75+m\angle F+120=540^\circ\\\Rightarrow m\angle F=125^\circ\\`

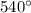
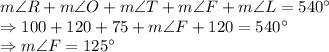
Due to similarity property of the two pentagons,
`\angle F =\angle G = 125^\circ`

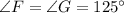
Part B:

Ratio of corresponding sides is equal.

Given the sides SU = 12, RO = 8 and FL = 10 units respectively.

`(SU)/(RO)=(AG)/(FL)\\(12)/(8)=(AG)/(10)\\\Rightarrow AG = 15\ units`

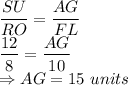
Part C:

Ratio of corresponding sides must be equal to ratio of perimeter of the two polygons:

`(RO)/(SU) = \frac{\text{perimeter of ROTFL}}{\text{perimeter of SUBAG}}\\\Rightarrow (8)/(12) = \frac{52}{\text{perimeter of SUBAG}}\\\Rightarrow \text{perimeter of SUBAG} = 52 * 1.5\\\Rightarrow \text{perimeter of SUBAG} = 78\ units`

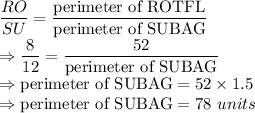
So, the answers are:

a)
`\angle G = 125^\circ`

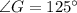
b) AG = 15 units

c) Perimeter of polygon SUBAG = 78 units