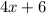Answer:
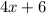 is the numerator.
is the numerator.
Explanation:
The given term is:
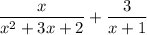
First of all, let us have a look at the denominator of the 1st term:
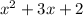
Factorizing by writing
 as
as
 and then taking 'x' and '1' common respectively:
and then taking 'x' and '1' common respectively:
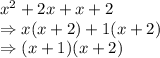
Now, solving the given expression by taking LCM:
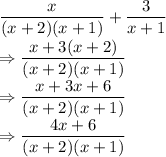
Any expression
 has
has
 as its numerator and
as its numerator and
 as its denominator.
as its denominator.
So, the numerator of simplified term is: