Question

What is the sum of the first 30 terms of this arithmetic sequence?
6,13, 20, 27, 34, ...

Answer 1

• The sum of the first 30 terms of this arithmetic sequence is 209. Hoped this helped.

Explanation:

We know that:

• Formula = 6 + (7x)

Work:

• => 6 + (7x)
• => 6 + {7(29)}
• => 6 + 203
• => 209

Hence, the sum of the first 30 terms of this arithmetic sequence is 209. Hoped this helped.

`BrainiacUser1357`

Answer 2

The sum of first 30 terms of arithmetic sequence is 3225.

Step-by-step explanation:

Here's the required formula to find the sum of the arithmetic sequence :

`\star{\underline{\boxed{\sf{S_n = (n)/(2)\Big[2a + (n - 1)d\Big]}}}}`

• 
  `\pink\star` Sₙ = number of terms of AP
• 
  `\pink\star` n = n terms of AP
• 
  `\pink\star` d = common difference of AP
• 
  `\pink\star` a = first term of AP

Substituting all the given values in the formula to find the sum of arithmetic sequence :

• 
  `\blue\star` Sₙ = 30
• 
  `\blue\star` n = 30
• 
  `\blue\star` d = 7
• 
  `\blue\star` a = 6

`{\implies{\sf{S_n = (n)/(2)\Big[2a + (n - 1)d\Big]}}}`

`{\implies{\sf{S_(30) = (30)/(2)\Big[2 * 6 + (30 - 1)7\Big]}}}`

`{\implies{\sf{S_(30) = (30)/(2)\Big[12+ (29)7\Big]}}}`

`{\implies{\sf{S_(30) = (30)/(2)\Big[12+ 29 * 7\Big]}}}`

`{\implies{\sf{S_(30) = (30)/(2)\Big[12+203\Big]}}}`

`{\implies{\sf{S_(30) = (30)/(2)\Big[ \: 215 \: \Big]}}}`

`{\implies{\sf{S_(30) = 15\Big[ \: 215 \: \Big]}}}`

`{\implies{\sf{S_(30) = 15 * 215}}}`

`{\implies{\sf{S_(30) = 3225}}}`

`\star{\underline{\boxed{\sf{S_(30) =3225}}}}`

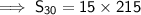
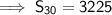
Hence, the sum of first 30 terms of arithmetic sequence is 3225.

`\rule{300}{2.5}`