Question

Toll booths on the New York State Thruway are often congested because of the large number of cars waiting to pay. A consultant working for the state concluded that if service times are measured from the time a car stops in line until it leaves, service times are exponentially distributed with a mean of 2.7 minutes. What proportion of cars can get through the toll booth in less than 3 minutes?

Answer 1

The proportion of cars can get through the toll booth in less than 3 minutes is 67%.

Explanation:

Let the random variable X be defined as the service times at a tool booth.

The random variable X follows an Exponential distribution with parameter μ = 2.7 minutes.

The probability density function of X is:

`f_(X)(x)=(1)/(\mu)e^(-x/\mu );\ x\geq 0,\ \mu>0`

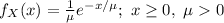
Compute the probability that a car can get through the toll booth in less than 3 minutes as follows:

`P(X<3)=\int\limits^(3)_(0) {(1)/(2.7)\cdot e^(-2.7x)} \, dx`

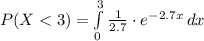
`=(1)/(2.7)\cdot \int\limits^(3)_(0) {e^(-x/2.7)} \, dx \\\\=(1)/(2.7)\cdot [-(e^(-x/2.7))/(1/2.7)]^(3)_(0)\\\\=1-e^(-3/2.7)\\\\=0.6708`

Thus, the proportion of cars can get through the toll booth in less than 3 minutes is 67%.