Question

A 0.20-kg block rests on a frictionless level surface and is attached to a horizontally aligned spring with a spring constant of 40 N/m. The block is initially displaced 4.0 cm from the equilibrium point and then released to set up a simple harmonic motion. A frictional force of 0.3 N exists between the block and surface. What is the speed of the block when it passes through the equilibrium point after being released from the 4.0-cm displacement point

Answer 1

Approximately
`0.45\; \rm m \cdot s^(-1)`.

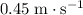Step-by-step explanation:

The mechanical energy of an object is the sum of its potential energy and kinetic energy. Consider this question from the energy point of view:

Mechanical energy of the block
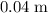`0.04\; \rm m` away from the equilibrium position:

• Elastic potential energy:
  `\displaystyle (1)/(2) \, k\, x^2 = (1)/(2)* \left(0.04\; \rm m\right)^2 * 40\; \rm N \cdot m^(-1) = 0.032\; \rm J`.
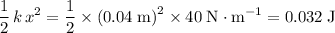• Kinetic energy:
  `0\; \rm J`.

While the block moves back to the equilibrium position, it keeps losing (mechanical) energy due to friction:

`\begin{aligned}& \text{Work done by friction} = (-0.3\; \rm N) * (0.04 \; \rm m) = -0.012\; \rm J\end{aligned}`.

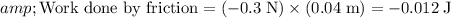The opposite (
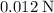`0.012\; \rm N`) of that value would be the amount of energy lost to friction. Since there's no other form of energy loss, the mechanical energy of the block at the equilibrium position would be
`0.032\; \rm N - 0.012\; \rm N = 0.020\; \rm N`.

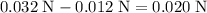The elastic potential energy of the block at the equilibrium position is zero. As a result, all that
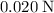`0.020\; \rm N` of mechanical energy would all be in the form of the kinetic energy of that block.

• Elastic potential energy:
  `0\; \rm J`.
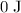• Kinetic energy:
  `0.020\; \rm J`.

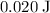Given that the mass of this block is
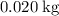`0.020\; \rm kg`, calculate its speed:

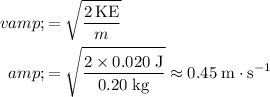`\begin{aligned}v &= \sqrt{\frac{2\, \mathrm{KE}}{m}} \\ &= \sqrt{(2 * 0.020\; \rm J)/(0.20\; \rm kg)} \approx 0.45\; \rm m\cdot s^(-1)\end{aligned}`.