Question

ANSWER FAST

please help me answer these following question A sample of the amount of rent paid for one-bedroom apartments of similar size near the University of Oregon are: $295, $475, $345, $595, $538, $460. A second sample of the amount of rent paid for one-bedroom apartments of similar size near the University of Washington are $495, $422, $370, $333, $370, $390. Using the Text Editor, answer the following questions: What is the median price of rent for the University of Oregon? What is the median price of rent for the University of Washington? What is the mean price of rent near the University of Oregon? What is the mean price of rent near the University of Washington? Describe the standard deviation for both Universities and explain how you determined this.

Answer 1

The mean, median, and standard deviation of the University of Oregon are $451.33, $467.5, and $113.61 respectively.

The mean, median, and standard deviation of the University of Washington are $396.67, $380, and $56.27 respectively.

Explanation:

We are given that a sample of the amount of rent paid for one-bedroom apartments of similar size near the University of Oregon is: $295, $475, $345, $595, $538, $460.

A second sample of the amount of rent paid for one-bedroom apartments of similar size near the University of Washington is: $495, $422, $370, $333, $370, $390.

Firstly, we will calculate the mean, median, and standard deviation for the data of the University of Oregon.

Arranging the data in ascending order we get;

X = $295, $345, $460, $475, $538, $595.

The mean of the above data is given by the following formula;

Mean,
`\bar X` =
`(\sum X)/(n)`

=
`(\$295+ \$345+ \$460+\$475+ \$538+\$595)/(6)`

=
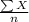
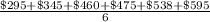
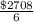`(\$2708)/(6)` = $451.33

So, the mean price of rent near the University of Oregon is $451.33.

For calculating the median, we first have to observe that the number of observations (n) in the data is even or odd.

• If n is odd, then the formula for calculating median is given by;

Median =
`((n+1)/(2) )^(th) \text{ obs.}`

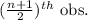
• If n is even, then the formula for calculating median is given by;

Median =
`\frac{((n)/(2) )^(th) \text{ obs. } + ((n)/(2)+1 )^(th) \text{ obs.}}{2}`

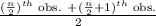
Here, the number of observations is even, i.e. n = 6.

So, Median =
`\frac{((n)/(2) )^(th) \text{ obs. } + ((n)/(2)+1 )^(th) \text{ obs.}}{2}`

=
`\frac{((6)/(2) )^(th) \text{ obs. } + ((6)/(2)+1 )^(th) \text{ obs.}}{2}`

=
`\frac{(3 )^(rd) \text{ obs. } + (4 )^(th) \text{ obs.}}{2}`

=
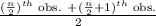
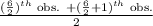
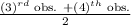
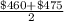`(\$460 +\$475)/(2)` = $467.5

Hence, the median price of rent for the University of Oregon is $467.5.

Now, the standard deviation is calculated by using the following formula;

Standard deviation, S.D. =
`\sqrt{(\sum (X -\bar X)^(2) )/(n-1) }`

=
`\sqrt{( (\$295 - \$451.33)^(2) +(\$345 - \$451.33)^(2) +......+(\$595 - \$451.33)^(2) )/(6-1) }`

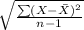
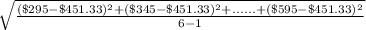
= $113.61

So, the standard deviation for the University of Oregon is $113.61.

Now, we will calculate the mean, median, and standard deviation for the data of the University of Washington.

Arranging the data in ascending order we get;

X = $333, $370, $370, $390, $422, $495.

The mean of the above data is given by the following formula;

Mean,
`\bar X` =
`(\sum X)/(n)`

=
`(\$333+ \$370+ \$370+\$390+ \$422+\$495)/(6)`

=
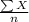
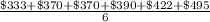
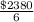`(\$2380)/(6)` = $396.67

So, the mean price of rent near the University of Washington is $396.67.

For calculating the median, we first have to observe that the number of observations (n) in the data is even or odd.

• If n is odd, then the formula for calculating median is given by;

Median =
`((n+1)/(2) )^(th) \text{ obs.}`

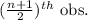
• If n is even, then the formula for calculating median is given by;

Median =
`\frac{((n)/(2) )^(th) \text{ obs. } + ((n)/(2)+1 )^(th) \text{ obs.}}{2}`

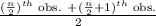
Here, the number of observations is even, i.e. n = 6.

So, Median =
`\frac{((n)/(2) )^(th) \text{ obs. } + ((n)/(2)+1 )^(th) \text{ obs.}}{2}`

=
`\frac{((6)/(2) )^(th) \text{ obs. } + ((6)/(2)+1 )^(th) \text{ obs.}}{2}`

=
`\frac{(3 )^(rd) \text{ obs. } + (4 )^(th) \text{ obs.}}{2}`

=
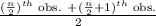
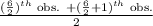
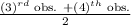
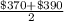`(\$370 +\$390)/(2)` = $380

Hence, the median price of rent for the University of Washington is $380.

Now, the standard deviation is calculated by using the following formula;

Standard deviation, S.D. =
`\sqrt{(\sum (X -\bar X)^(2) )/(n-1) }`

=
`\sqrt{( (\$333 - \$396.67)^(2) +(\$370 - \$396.67)^(2) +......+(\$495 - \$396.67)^(2) )/(6-1) }`

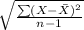
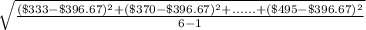
= $56.27

So, the standard deviation for the University of Washington is $56.27.