Answer:
Answer B: "half as much as before"
Step-by-step explanation:
Consider the conservation of momentum to start with in order to find the velocity of the conglomerate of the two cars after collision:

With this important result, we can nor compare the initial kinetic energy to the final one:
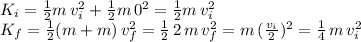
Therefore, the final kinetic energy is one half of the initial kinetic energy.