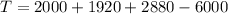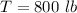Answer:
The total amount is
Step-by-step explanation:
from the question we are told that
The initial mas of water in the tank is

The mass flow rate of the hot water inlet pipe is
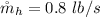
The mass flow rate of the cold water inlet pipe is

The mass flow rate of the exit pipe is
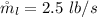
The time being considered is
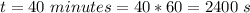
The amount of water deposited by the hot inlet pipe in 40 minutes is mathematically represented as
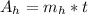
substituting values

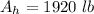
The amount of water deposited by the cold inlet pipe in 40 minutes is mathematically represented as
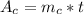
substituting values
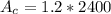
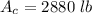
The total amount of water that let the tank after 40 \minutes is

substituting values

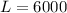
The total amount of water in the tank after 40 minutes is
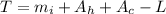
substituting values