Answer:
The farmer can achieve a maximum area of 50 square yards with 20 yards of fencing.
Explanation:
Given that farmer shall construct a rectangular fenced-in area and a side of the barn is one side of such area, the needed length of fencing is represent by the following perimeter equation (
 ), measured in square yards:
), measured in square yards:
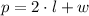
Where:
 - Length of the rectangle, measured in yards.
- Length of the rectangle, measured in yards.
 - Width of the rectangule (side of the barn), measured in yards.
- Width of the rectangule (side of the barn), measured in yards.
In addition, the equation of the fenced-in area (
 ) is:
) is:
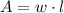
If
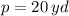 , equation of area is now simplified as follows:
, equation of area is now simplified as follows:
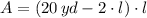
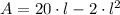
The value of
 associated with the maximum area is obtained with the help of First and Second Derivative Tests. Firstly, first and second derivatives of the area function are determined:
associated with the maximum area is obtained with the help of First and Second Derivative Tests. Firstly, first and second derivatives of the area function are determined:
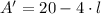
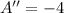
Let equalize first equation to zero, second derivative indicates that critical value follows to an absolute maximum. Hence:
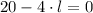
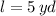
The width of the rectangle is: (
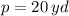 and
and
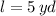 )
)
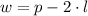

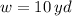
And finally, the maximum area she can achieve is:
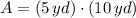

The farmer can achieve a maximum area of 50 square yards with 20 yards of fencing.