Question

A simple random sample of size nequals15 is drawn from a population that is normally distributed. The sample mean is found to be x overbarequals18.3 and the sample standard deviation is found to be sequals6.3. Determine if the population mean is different from 24 at the alpha equals 0.01 level of significance. Complete parts ​(a) through ​(d) below.

​(a) Determine the null and alternative hypotheses. Upper H 0​: ▼ p sigma mu ▼ less than not equals equals greater than 24 Upper H 1​: ▼ sigma mu p ▼ greater than not equals equals less than 24 ​
(b) Calculate the​ P-value.​P-valueequals nothing ​(Round to three decimal places as​ needed.)​
(c) State the conclusion for the test.
A. Do not reject Upper H 0 because the​ P-value is less than the alphaequals0.01 level of significance.
B. Do not reject Upper H 0 because the​ P-value is greater than the alphaequals0.01 level of significance.
C. Reject Upper H 0 because the​ P-value is less than the alphaequals0.01 level of significance.
D. Reject Upper H 0 because the​ P-value is greater than the alphaequals0.01 level of significance.
​(d) State the conclusion in context of the problem. There ▼ is not is sufficient evidence at the alpha equals 0.01 level of significance to conclude that the population mean is different from 24.

Answer 1

(a) Null Hypothesis,
`H_0` :
`\mu` = 24

Alternate Hypothesis,
`H_A` :
`\mu\\eq` 24

(b) The​ P-value is 0.004.

(c) Reject Upper H 0 because the​ P-value is less than the alpha = 0.01 level of significance.

(d) There is sufficient evidence at the alpha equals 0.01 level of significance to conclude that the population mean is different from 24.

Explanation:

We are given that a simple random sample of size n = 15 is drawn from a population that is normally distributed. The sample mean is found to be x overbar = 18.3 and the sample standard deviation is found to be s = 6.3.

Let
`\mu` = population mean

(a) Null Hypothesis,
`H_0` :
`\mu` = 24 {means that the population mean is 24}

Alternate Hypothesis,
`H_A` :
`\mu\\eq` 24 {means that the population mean is different from 24}

The test statistics that will be used here is One-sample t-test statistics because we don't know about population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean = 18.3

s = sample standard deviation = 6.3

n = sample size = 15

So, the test statistics =
`(18.3-24)/((6.3)/(√(15) ) )` ~
`t_1_4`

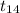
= -3.504

The value of t-test statistics is -3.504.

(b) Now, the P-value of the test statistics is given by;

P-value = P(
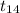`t_1_4` < -3.504) = 0.002 or 0.2%

For the two-tailed test, the P-value is calculated as =
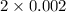`2 * 0.002` = 0.004 or 0.4%.

(c) Since the p-value of the test statistics is less than the level of significance as 0.002 < 0.01, so we will reject our null hypothesis.

(d) This means that we have sufficient evidence at the alpha equals 0.01 level of significance to conclude that the population mean is different from 24.