Answer:
Explanation:
To put a quadratic into vertex form, you need to complete the square on it. Do this by following these steps. I'll tell you what we're doing and then show you what it looks like.
First step is to set the quadratic equal to 0 and then move the constant over. That's 2 steps in one, but not confusing at all. That looks like this:

Next, the rule is that the leading coefficient has to be a positive 1. Ours is a 2, so we will factor out a 2 but only from the left side. That looks like this:
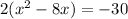
Next step is to take half the linear term (the number with the x attached to it, not the x-squared), square it, and add it in to both sides. This is where things get a bit tricky, so pay attention. Our linear term is 8, half of 8 is 4, and 4 squared is 16. So we add 16 in. We'll do it to the left only first:
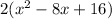
That's the left side. Notice that there is still a 2 out front there. That 2 is a multiplier. That means that what we actually added in was 2(16) = 32, not just 16. Now adding that to the right makes the whole thing:
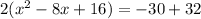
Completing the square allows us to create a perfect square binomial on the left which is in the form (x - )². That blank space is filled in with the number we squared and then added in. We squared a 4 to get 16, so our perfect square binomial is (x - 4)². Putting that together:
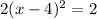
Last step is to move the constant back over and set the quadratic back equal to y:
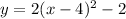
From here the vertex is apparent. It is (4, -2).