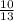Answer:
(a)
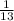
(b)
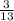
(c)
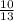
Explanation:
The probability of an event B occurring is given by;
P(B) =
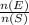
Where;
P(B) = probability of the event B
n(E) = number of favourable outcomes
n(S) = total number of events in the sampled space.
From the question, the card is drawn randomly from a standard 52-card deck. The probability of
(a) drawing a "king" card is analyzed as follows.
Let the event of drawing the "king" card be B.
In a standard 52-card deck, the number of cards that are of type king is 4. i.e 1 from the diamond pack, 1 from the spade pack, 1 from the heart pack and 1 from the club pack.
Therefore, the number of favourable outcomes is 4, while the total number of events in the sampled space is 52.
The probability of drawing a "king" card, P(B) is;
P(B) =
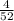
P(B) =
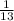
(b) drawing a "face" card is analyzed as follows.
Let the event of drawing the "face" card be B.
In a standard 52-card deck, a face card can either be a Jack, Queen or a King. There are 4 Jack cards, 4 Queen cards and 4 King cards in the deck. The number of cards that are of type face is 12.
Therefore, the number of favourable outcomes is 12, while the total number of events in the sampled space is 52.
The probability of drawing a "face" card, P(B) is;
P(B) =
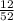
P(B) =
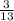
(c) drawing a card that is not a "face" is analyzed as follows;
The sum of the probability of drawing a face card and the probability of not drawing a face card is always 1.
Let the event of drawing a "face" card be B and the event of not drawing a "face" card be C.
P(B) + P(C) = 1
P(C) = 1 - P(B)
From (b) above, the P(B) =
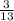
Therefore,
P(C) = 1 -
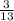
P(C) =