Question

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part. Tutorial Exercise Find the derivative of the function.

y = 81 arcsin x 9 − x 81 − x2.

Answer 1

`(d)/(dx)[f(x)+g(x)+h(x)] = \frac{9\cdot x^(8)}{\sqrt{1-x^(18)}} - 81\cdot x^(80)-2\cdot x`

Explanation:

This derivative consist in the sum of three functions:
`f(x) = 81\cdot \sin^(-1) x^(9)`,
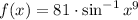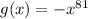`g(x) = - x^(81)` and
`h(x) = - x^(2)`. According to differentiation rules, the derivative of a sum of functions is the same as the sum of the derivatives of each function. That is:

`(d)/(dx) [f(x)+g(x) + h(x)] = (d)/(dx) [f(x)]+(d)/(dx) [g(x)] +(d)/(dx) [h(x)]`

Now, each derivative is found by applying the derivative rules when appropriate:

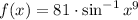`f(x) = 81\cdot \sin^(-1) x^(9)` Given

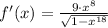`f'(x) = \frac{9\cdot x^(8)}{\sqrt{1-x^(18)}}` (Derivative of a arcsine function/Chain rule)

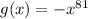`g(x) = - x^(81)` Given

`g'(x) = -81\cdot x^(80)` (Derivative of a power function)

`h(x) = - x^(2)` Given

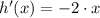`h'(x) = -2\cdot x` (Derivative of a power function)

`(d)/(dx)[f(x)+g(x)+h(x)] = \frac{9\cdot x^(8)}{\sqrt{1-x^(18)}} - 81\cdot x^(80)-2\cdot x` (Derivative for a sum of functions/Result)