Question

Suppose ADequalsISubscript m ​(the mtimesm identity​ matrix). Show that for any Bold b in set of real numbers R Superscript m​, the equation ABold xequalsBold b has a solution.​ [Hint: Think about the equation ADBold bequalsBold b​.] Explain why A cannot have more rows than columns.

Answer 1

See Explanation

Explanation:

(a)For matrices A and D, given that:
`AD=I_m`.

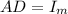We want to show that
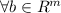`\forall b \in R^m`, Ax=b has a solution.

If Ax=b

Multiply both sides by D

`(Ax)D=b * D\\\implies (AD)x=bD$ (Recall: AD=I_m)\\\implies I_mx=Db $ (Since I_m$ is the m* m$ identity matrix)\\\implies x=Db`

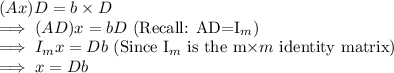
This means that the system Ax=b has a solution.

(b)Matrix A has a pivot position in each row where each pivot is a different column. Therefore, A must have at least as many columns as rows.

This means A cannot have more rows than columns.