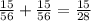Answer:
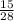 is the required probability.
is the required probability.
Explanation:
Total number of Marbles = Blue + Red
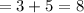
Probability of getting blue
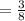
Probability of not getting a blue
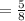
To get exactly one blue in two draws, we either get a blue, not blue, or a not blue, blue.
First Draw Blue, Second Draw Not Blue:
1st Draw:
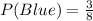
2nd Draw:
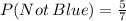 (since we did not replace the first marble)
(since we did not replace the first marble)
To get the probability of the event, since each draw is independent, we multiply both probabilities.
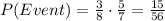
First Draw Not Blue, Second Draw Not Blue:
1st Draw:
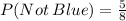
2nd Draw:
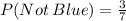 (since we did not replace the first marble)
(since we did not replace the first marble)
To get the probability of the event, since each draw is independent, we multiply both probabilities.
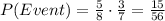
To get the probability of exactly one blue, we add both of the events: