Question

Support requests arrive at a software company at the rate of 1 every 30 minutes. Assume that the requests arrive as events in a Poisson process.

a) What is the probability that the number of requests in an hour is between 2 and 4 inclusive? Give your answer to four decimal places.

b) What is the expected number of requests in a 10 hour work day? Give an exact answer.

c) What is the probability that the number of requests in a 10 hour work day is between 20 and 24 inclusive? Give your answer to four decimal places.

d) What is the standard deviation of the number of requests in a 10 hour work day? Give your answer to four decimal places.

Answer 1

a. 0.5413

b. 20

c. 0.3724

d. 4.4721

Explanation:

Solution:-

- We will start by defining a random variable X.

X : The number of support requests arrived

- The event defined by the random variable ( X ) is assumed to follow Poisson distribution. This means the number of request in two distinct time intervals are independent from one another. Also the probability of success is linear within a time interval.

- The time interval is basically the time required for a poisson event to occur. Consequently, each distributions is defined by its parameter(s).

- Poisson distribution is defined by " Rate at which the event occurs " - ( λ ). So in our case the rate at which a support request arrives in a defined time interval. We define our distributions as follows:

X ~ Po ( λ )

Where, λ = 1 / 30 mins

Hence,

X ~ Po ( 1/30 )

a)

- We see that the time interval for events has been expanded from 30 minutes to 1 hour. However, the rate ( λ ) is given per 30 mins. In such cases we utilize the second property of Poisson distribution i.e the probability of occurrence is proportional within a time interval. Then we scale the given rate to a larger time interval as follows:

λ* =
`(1)/((1)/(2) hr) = (2)/(1hr)`

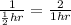
- We redefine our distribution as follows:

X ~ Po ( 2/1 hr )

- Next we utilize the probability density function for poisson process and accumulate the probability for 2 to 4 request in an hour.

`P ( X = x ) = (e^-^l^a^m^b^d^a . lambda^x)/(x!)`

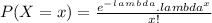
- The required probability is:

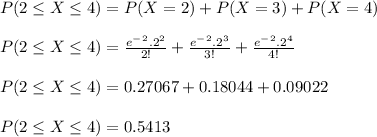`P ( 2 \leq X \leq 4 ) = P ( X = 2 ) + P ( X = 3 ) + P ( X = 4 )\\\\P ( 2 \leq X \leq 4 ) = (e^-^2 . 2^2)/(2!) + (e^-^2 . 2^3)/(3!) + (e^-^2 . 2^4)/(4!)\\\\P ( 2 \leq X \leq 4 ) = 0.27067 + 0.18044 + 0.09022\\\\P ( 2 \leq X \leq 4 ) = 0.5413` Answer

b)

We will repeat the process we did in the previous part and scale the poisson parameter ( λ ) to a 10 hour work interval as follows:

λ* =
`(2)/(1 hr) * (10)/(10) = (20)/(10 hr)`

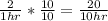
- The expected value of the poisson distribution is given as:

E ( X ) = λ

Hence,

E ( X ) = 20 (10 hour work day) .... Answer

c)

- We redefine our distribution as follows:

X ~ Po ( 20/10 hr )

- Next we utilize the probability density function for poisson process and accumulate the probability for 20 to 24 request in an 10 hour work day.

`P ( X = x ) = (e^-^l^a^m^b^d^a . lambda^x)/(x!)`

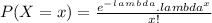
- The required probability is:

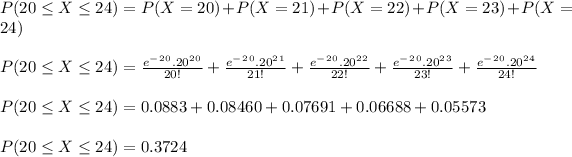`P ( 20 \leq X \leq 24 ) = P ( X = 20 ) + P ( X = 21 ) + P ( X = 22 )+P ( X = 23 ) + P ( X = 24 )\\\\P ( 20 \leq X \leq 24 ) = (e^-^2^0 . 20^2^0)/(20!) + (e^-^2^0 . 20^2^1)/(21!) + (e^-^2^0 . 20^2^2)/(22!) + (e^-^2^0 . 20^2^3)/(23!) + (e^-^2^0 . 20^2^4)/(24!) \\\\P ( 20 \leq X \leq 24 ) = 0.0883 +0.08460 +0.07691 +0.06688+0.05573\\\\P ( 20 \leq X \leq 24 ) = 0.3724` Answer

c)

The standard deviation of the poisson process is determined from the application of Poisson Limit theorem. I.e Normal approximation of Poisson distribution. The results are:

σ = √λ

σ = √20

σ = 4.4721 ... Answer