Question

A particular fruit's weights are normally distributed, with a mean of 476 grams and a standard deviation of 36 grams. The heaviest 19% of fruits weigh more than how many grams? Give your answer to the nearest gram.

Answer 1

Explanation:

Given that:

mean (μ) = 476 grams, standard deviation (σ) = 36 grams. P(z) = 19%

The z score shows by how many standard deviation the raw score is above or below the mean. It is given by the equation:

`z=(x-\mu)/(\sigma)`

Since the 19% weigh more, therefore 81% (100% - 19%) weigh less.

From the normal distribution table, the z score that corresponds to a probability of 81%(0.81) = 0.87

We substitute z = 0.88 in the z score equation to find the raw score. Therefore:

`z=(x-\mu)/(\sigma)\\0.87=(x-476)/(36)\\ x-476=31.32\\x=31.32+476\\x=507.32\\`

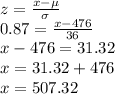
x ≅ 507 grams

Therefore 19% of fruits weigh more than 507 grams