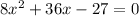Question

Α' β

5. A quadratic equation 2x2 = 6x + 3 has two roots p and q. Find the quadratic equations with
roots p2q and pq2?
​

Answer 1

8x² +36x -27=0

Explanation:

2x²= 6x +3

Let's rewrite the equation into the form of ax²+bx+c= 0.

2x² -6x -3=0

Thus, a= 2

b= -6

c= -3

Sum of roots=
`- (b)/(a)`

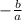
Since your roots are p and q, sum of roots= p +q

p +q=
`- (( - 6)/(2) )`

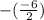
p +q= 6 ÷2

p +q= 3

Product of roots=
`(c)/(a)`

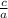
pq=
`- (3)/(2)`

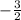
Quadratic equations:

x² -(sum of roots)x +(product of roots)= 0

Thus, we have to find the sum and the product of the new roots, p²q and pq².

p +q= 3

pq= -3/2

Product of new roots

= (p²q)(pq²)

= p³q³

= (pq)³

`= ( - (3)/(2) )^(3) \\ = - (27)/(8)`

sum of new roots

= p²q +pq²

= pq(p +q)

= (-3/2)(3)

= -9/2

Thus, the quadratic equation with roots p²q and pq² is

x² -(-9/2)x -27/8 = 0

`x ^(2) + (9)/(2) x - (27)/(8) = 0`

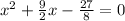
Multiply by 8 throughout:

`8 {x}^(2) + 36x - 27 = 0`