Answer:
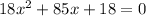
Explanation:
Given Equation is
=>
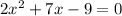
Comparing it with
 , we get
, we get
=> a = 2, b = 7 and c = -9
So,
Sum of roots = α+β =
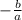
α+β = -7/2
Product of roots = αβ = c/a
αβ = -9/2
Now, Finding the equation whose roots are:
α/β ,β/α
Sum of Roots =
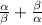
Sum of Roots =
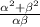
Sum of Roots =
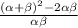
Sum of roots =

Sum of roots =
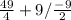
Sum of Roots =
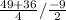
Sum of roots =
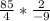
Sum of roots = S =
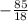
Product of Roots =
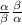
Product of Roots = P = 1
The Quadratic Equation is:
=>
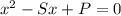
=>
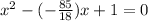
=>
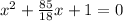
=>
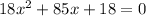
This is the required quadratic equation.