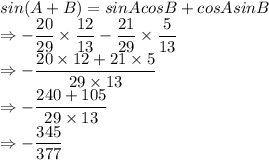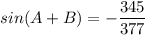Question

You are given that sin(A)=−20/29, with A in Quadrant III, and cos(B)=12/13, with B in Quadrant I. Find sin(A+B). Give your answer as a fraction.

Answer 1

`sin(A+B)=-(345)/(377)`

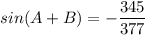
Explanation:

Given that:

`sin(A)=-(20)/(29)\\cos(B)=(12)/(13)`

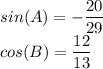
A is in 3rd quadrant and B is in 1st quadrant.

To find: sin(A+B)

Solution:

We know the Formula:

1.
`sin(A+B) = sinAcosB+cosAsinB`

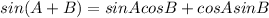
2.
`sin^(2) \theta+cos^(2) \theta=1`

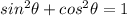
Now, let us find the values of cosA and sinB.

`sin^(2) A+cos^(2) A=1\\\Rightarrow ((-20)/(29))^2+cos^(2) A=1\\\Rightarrow cos^(2) A=1- (400)/(941)\\\Rightarrow cos^(2) A=(941-400)/(941)\\\Rightarrow cos^(2) A=(441)/(941)\\\Rightarrow cos A=\pm (21)/(29)`

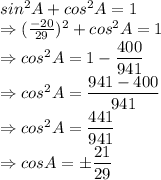
A is in 3rd quadrant, so cosA will be negative,

`\therefore cos A=-(21)/(29)`

`sin^(2) B+cos^(2) B=1\\\Rightarrow sin^(2) A+((12)/(13))^2=1\\\Rightarrow sin^(2) B=1- (144)/(169)\\\Rightarrow sin^(2) B=(169-144)/(169)\\\Rightarrow sin^(2) B=(25)/(169)\\\Rightarrow sinB=\pm (5)/(13)`

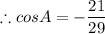
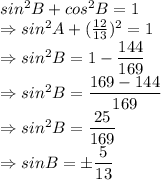
B is in 1st quadrant, sin B will be positive.

`sinB =(5)/(13)`

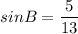
Now, using the formula:

`sin(A+B) = sinAcosB+cosAsinB\\\Rightarrow -(20)/(29) * (12)/(13)-(21)/(29)* (5)/(13)\\\Rightarrow -(20* 12+21* 5)/(29* 13) \\\Rightarrow -(240+105)/(29* 13) \\\Rightarrow -(345)/(377)`

`sin(A+B)=-(345)/(377)`