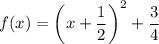Answer:
Step-by-step explanation:
We are given the function:
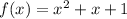 .
.
And we want to turn this into vertex form.
Note that our given function is in the standard form:

In other words, a = 1, b = 1, and c = 1.
To convert from standard form to vertex form, we can either: (1) complete the square, or (2) find the vertex manually.
In most cases, the second method is more time efficient.
Vertex form is given by:
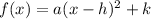
Where a is the leading coefficient and (h, k) is the vertex.
We have already determined that a = 1.
Find the vertex. The x-coordinate of the vertex of a quadratic is given by:
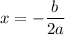
Therefore, our point is:
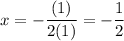
To find the y-coordinate or k, substitute this value back into the function:
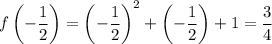
Thus, the vertex is (-1/2, 3/4). So, h = -1/2 and k = 3/4.
Hence, the vertex form is:
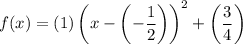
Simplify: