This is a perfect example of exponential decay. In this case the growth factor should be represented by a fraction, and it is! This forest, starting out with apparently ( 800? ) pine trees, has a disease spreading, which kills 1 / 4th of each of the pine trees yearly. Therefore, the pine trees remaining should be 3 / 4.
Respectively 3 / 4 should be the growth factor, starting with 800 pine trees - the start value. This can be represented as such,
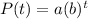 - where a = start value, b = growth factor, t = time ( variable quantity )
- where a = start value, b = growth factor, t = time ( variable quantity )
____
Thus, the function
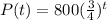 can model this problem. The forest after t years should have P( t ) number of pine trees remaining.
can model this problem. The forest after t years should have P( t ) number of pine trees remaining.