Question

Find the smallest perimeter and the dimensions for a rectangle with an area of 2525 in. squared g

Answer 1

5 in x 5 in

Explanation:

The area of the rectangle is given by:

`A=x*y=25\\y=(25)/(x)`

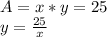
Where x and y are the length and width of the rectangle.

The perimeter is:

`P=2x+2y\\P=2x+2*(25)/(x)\\ P=2x+(50)/(x)`

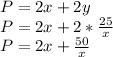
The value of x for which the derivate of the perimeter function is zero is the length that yields the smallest perimeter:

`P=2x+(50)/(x) \\\\P'=2-(50)/(x^2) =0\\2x^2=50\\x=5\ in`

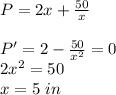
The value of y is:

`y=(25)/(5)\\y=5\ in`

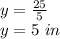
Therefore, the dimensions that yield the smallest perimeter are 5 in x 5 in.