Question

Eliana wants to estimate the number of out of state visitors at a national park. She surveys 200 visitors and finds that 83 of them are from out of state. Identify the values needed to calculate a confidence interval at the 90% confidence level. Then find the confidence interval.

Answer 1

The 90% confidence interval for the proportion of out of state visitors at a national park is (0.3577, 0.4723).

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

For this problem, we have that:

`n = 200, \pi = (83)/(200) = 0.415`

90% confidence level

So
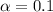`\alpha = 0.1`, z is the value of Z that has a pvalue of
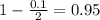`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

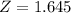The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.415 - 1.645\sqrt{(0.415*0.585)/(200)} = 0.3577`

The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.415 + 1.645\sqrt{(0.415*0.585)/(200)} = 0.4723`

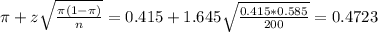
The 90% confidence interval for the proportion of out of state visitors at a national park is (0.3577, 0.4723).