Answer:
Anxiety score close to 54.58.
Explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question:

Approximately what anxiety test score would put someone in the top 5 percent?
We have to find the 100 - 5 = 95th percentile, which is X when Z has a pvalue of 0.95. So X when Z = 1.645.

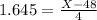

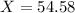
Anxiety score close to 54.58.