Complete question:
A consumer products company is formulating a new shampoo and is interested in foam height (in millimeters). Foam height is approximately normally distributed and has a standard deviation of 20 millimeters. The company wishes to test H0: u=175 millimeters versus Ha:u>175 millimeters, using the results of n samples. Find the boundary of the critical region if the type I error probability is
 and n = 16
and n = 16
Answer:
186.63
Explanation:
Given:

Using the standard normal deviate table:
NORMSINV(0.01) = 2.326
Thus, the Z score = 2.326
To find the critical value if the mean, use the formula:
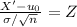
Since we are to find X', Make X' subject of the formula:
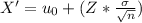
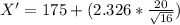

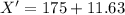
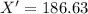
The boundary of the critical region is 186.63