Answer:
The tension on the rope is T = 900 N
Step-by-step explanation:
From the question we are told that
The mass of the person on the left is
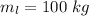
The force of the person on the left is
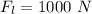
The mass of the person on the right is
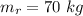
The force of the person on the right is
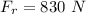
Generally the net force is mathematically represented as
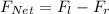
substituting values
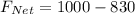
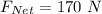
Now the acceleration net acceleration of the rope is mathematically evaluated as
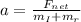
substituting values

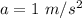
The force
 ) of the person on the left that caused the rope to accelerate by a is mathematically represented as
) of the person on the left that caused the rope to accelerate by a is mathematically represented as

Where T is the tension on the rope
substituting values

=> T = 900 N