Answer:
The heat rate produced from the motor is 84.216 watts.
Step-by-step explanation:
The electric motor receives power from electric current and releases power in the form of mechanical energy (torque) and waste heat and can be considered an stable-state system. The model based on the First Law of Thermodynamics for the electric motor is:

Where:
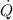 - Heat transfer from the electric motor, measured in watts.
- Heat transfer from the electric motor, measured in watts.
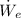 - Electric power, measured in watts.
- Electric power, measured in watts.
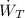 - Mechanical power, measured in watts.
- Mechanical power, measured in watts.
The heat transfer rate can be calculated in terms of electric and mechanic powers, that is:
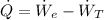
The electric and mechanic powers are represented by the following expressions:
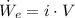
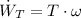
Where:
 - Current, measured in amperes.
- Current, measured in amperes.
 - Steady-state voltage, measured in volts.
- Steady-state voltage, measured in volts.
 - Torque, measured in newton-meters.
- Torque, measured in newton-meters.
 - Angular speed, measured in radians per second.
- Angular speed, measured in radians per second.
Now, the previous expression for heat transfer rate is expanded:
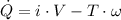
The angular speed, measured in radians per second, can be obtained by using the following expression:
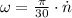
Where:
 - Rotational rate of change, measured in revolutions per minute.
- Rotational rate of change, measured in revolutions per minute.
If
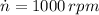 , then:
, then:
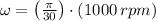
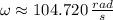
Given that
 ,
,
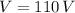 ,
,
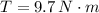 and
and
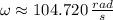 , the heat transfer rate from the electric motor is:
, the heat transfer rate from the electric motor is:
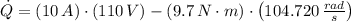
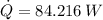
The heat rate produced from the motor is 84.216 watts.