Question

In a local ice sculpture contest, one group sculpted a block into a rectangular based pyramid. The dimensions of the base were 3 m by 5 m, and the pyramid was 3.6 m high. Calculate the amount of ice needed for this sculpture. A conical-shaped umbrella has a radius of 0.4 m and a height of 0.45 m. Calculate the amount of fabric needed to manufacture this umbrella. (Hint: an umbrella will have no base) A cone has a volume of 150 cm3 and a base with an area of 12 cm2. What is the height of the cone? Find the dimensions of a deck which will have railings on only three sides. There is 28 m of railing available and the deck must be as large as possible. A winter recreational rental company is fencing in a new storage area. They have two options. They can set it up at the back corner of the property and fence it in on four sides. Or, they can attach it to the back of their building and fence it in on three sides. The rental company has decided that the storage area needs to be 100 m2 if it is in the back corner or 98 m2 if it is attached to the back of the building. Determine the optimal design for each situation.

Answer 1

1. The amount of ice needed for the sculpture is 18 m³

2. The amount of fabric needed to manufacture the umbrella is 0.757 m²

3. The height of the cone is 37.5 cm

4. The largest possible storage area which is obtained by attaching the storage area to the back of the building is 87.11 m²

Explanation:

1. The volume, V, of a rectangular pyramid =
`(1)/(3) \cdot B \cdot h`

Where:

B = Base area = Length, L × Width, W

h = Height of the pyramid = 3.6 m

L = 5 m

W = 3 m

The volume = 1/3 × 5 × 3 × 3.6 = 18 m³

The amount of ice needed for the sculpture is 18 m³

2) The surface area of a cone = π·r·s

s = Slant height

r = Radius of the cone's base = 0.4 m

h = The height of the cone = 0.45m

s = √(0.4² + 0.45²) = (√145)/20

The surface area of the cone = π × 0.4 × (√145)/20 = 0.757 m²

The amount of fabric needed to manufacture the umbrella is 0.757 m²

3) The volume, V of the cone = 150 cm³

The base area,
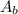`A_b`, of the cone = 12 cm²

The height of the cone = h

We note that the volume of a cone =
`(1)/(3) \cdot A_b \cdot h`

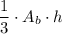
Therefore;

`(1)/(3) * 12 * h = 150`

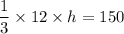
4·h = 150

h = 150/4 = 37.5 cm

The height of the cone = 37.5 cm

4) The storage area at the back corner with four sides = 100 m²

The storage area at the back of the building with three sides = 98 m²

Given that the available riling = 28 m, we have;

For maximum area the four sides should be equal, hence dimension of each side = 28/4 = 7

The area of storage space that can be fenced on four sides at the back corner = 7 × 7 = 49 m²

At the back of the building only three sides need fencing, we therefore have;

The side length = 28/3 =
`9(1)/(3)`

The area fenced =
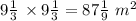`\left 9(1)/(3) \right * 9(1)/(3) = 87(1)/(9) \ m^2` = 87.11 m²

Therefore, the largest possible storage area, 87.11 m², is obtained by attaching the storage area to the back of the building.