Answer:
60% probability that the commuting time will be less than 70 minutes
Step-by-step explanation:
An uniform probability is a case of probability in which each outcome is equally as likely.
For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.
The probability that we find a value X lower than x is given by the following formula.
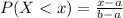
Suppose that the actual commuting time is uniformly distributed between 64 and 74 minutes.
This means that
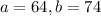
What is the probability that the commuting time will be less than 70 minutes
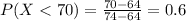
60% probability that the commuting time will be less than 70 minutes