Question

"A researcher wants to test if the mean G.P.A. of CC students transferring to Sac State is above 3.3. She randomly samples 25 CC students and finds that their average G.P.A. is 3.45. Assuming that the standard deviation of G.P.A.’s is 0.5, what can the researcher conclude at the 5% significance level

Answer 1

We failed to reject H₀

t < 2.06

1.5 < 2.06

We do not have significant evidence at significance level α=0.05 to show that the mean G.P.A. of CC students transferring to Sac State is above 3.3

Explanation:

Set up hypotheses:

Null hypotheses = H₀: μ = 3.3

Alternate hypotheses = H₁: μ > 3.3

Determine type of test:

Since the alternate hypothesis states that mean G.P.A. of CC students transferring to Sac State is above 3.3, therefore we will use a upper-tailed test.

Select the test statistic:

Since the sample size is very small (n < 30) therefore, we will use t-distribution.

Determine level of significance and critical value:

Given level of significance = 5% = 0.05

Since it is a upper tailed test,

At α = 0.05 and DF = n – 1 = 25 - 1 = 24

t-score = 2.06

Set up decision rule:

Since it is a upper tailed test, using a t statistic at a significance level of 5%

We Reject H₀ if t > 2.06

Compute the test statistic:

`$ t = \frac{\bar{x}-\mu}{(s)/(√(n) ) } $`

`$ t = ( 3.45- 3.3 )/((0.5)/(√(25) ) ) $`

`t = 1.5`

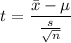
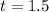
Conclusion:

We failed to reject H₀

t < 2.06

1.5 < 2.06

We do not have significant evidence at significance level α=0.05 to show that the mean G.P.A. of CC students transferring to Sac State is above 3.3