Question

Complete the identity.
1) sec^4 x + sec^2 x tan^2 x - 2 tan^4 x = ?

Answer 1

See Explanation

Explanation:

Question like this are better answered if there are list of options; However, I'll simplify as far as the expression can be simplified

Given

`sec^4 x + sec^2 x tan^2 x - 2 tan^4 x`

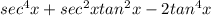
Required

Simplify

`(sec^2 x)^2 + sec^2 x tan^2 x - 2 (tan^2 x)^2`

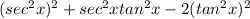
Represent
`sec^2x` with a

Represent
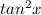`tan^2x` with b

The expression becomes

`a^2 + ab- 2 b^2`

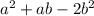
Factorize

`a^2 + 2ab -ab- 2 b^2`

`a(a + 2b) -b(a+ 2 b)`

`(a -b) (a+ 2 b)`

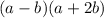
Recall that

`a = sec^2x`

`b = tan^2x`

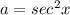
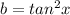
The expression
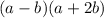`(a -b) (a+ 2 b)` becomes

`(sec^2x -tan^2x) (sec^2x+ 2 tan^2x)`

..............................................................................................................................

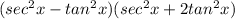
In trigonometry

`sec^2x =1 +tan^2x`

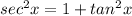
Subtract
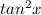`tan^2x` from both sides

`sec^2x - tan^2x =1 +tan^2x - tan^2x`

`sec^2x - tan^2x =1`

..............................................................................................................................

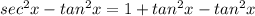
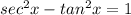
Substitute 1 for
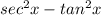`sec^2x - tan^2x` in
`(sec^2x -tan^2x) (sec^2x+ 2 tan^2x)`

`(1) (sec^2x+ 2 tan^2x)`

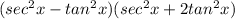
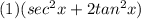
Open Bracket

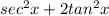`sec^2x+ 2 tan^2x` ------------------This is an equivalence

`(secx)^2+ 2 (tanx)^2`

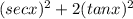
Solving further;

................................................................................................................................

In trigonometry

`secx = (1)/(cosx)`

`tanx = (sinx)/(cosx)`

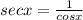
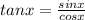
Substitute the expressions for secx and tanx

................................................................................................................................

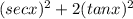`(secx)^2+ 2 (tanx)^2` becomes

`((1)/(cosx))^2+ 2 ((sinx)/(cosx))^2`

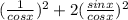
Open bracket

`(1)/(cos^2x)+ 2 ((sin^2x)/(cos^2x))`

`(1)/(cos^2x)+ (2sin^2x)/(cos^2x)`

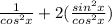
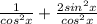
Add Fraction

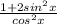`(1 + 2sin^2x)/(cos^2x)` ------------------------ This is another equivalence

................................................................................................................................

In trigonometry

`sin^2x + cos^2x= 1`

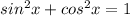
Make
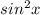`sin^2x` the subject of formula

`sin^2x= 1 - cos^2x`

................................................................................................................................

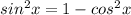
Substitute the expressions for
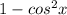`1 - cos^2x` for
`sin^2x`

`(1 + 2(1 - cos^2x))/(cos^2x)`

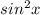
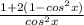
Open bracket

`(1 + 2 - 2cos^2x)/(cos^2x)`

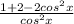
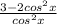`(3 - 2cos^2x)/(cos^2x)` ---------------------- This is another equivalence