The half-life of radioactive substance X is approximately 5,776 x 10³ years. With a decay constant resembling carbon-14, it's suitable for dating ancient objects, offering reliable age estimations.
1. The decay of the radioactive substance X is described by the equation
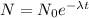 , where N is the number of atoms present,
, where N is the number of atoms present,
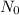 is the number of initial atoms,
is the number of initial atoms,
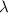 is the decay constant, and t is time.
is the decay constant, and t is time.
2. To find the decay constant
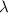 , you use the given data point:
, you use the given data point:
 , and
, and
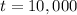 years.
years.
3. Substitute these values into the decay equation:
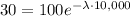 .
.
4. Solve for
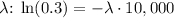 .
.
5. Calculate
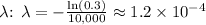 .
.
6. The average life time
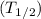 is given by
is given by
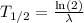 .
.
7. Substitute the value of
 years.
years.
This calculated half-life is close to that of carbon-14, indicating its suitability for dating ancient objects.
The half-life of the radioactive isotope substance X is calculated to be approximately 5,776 x 10³ years. This value, similar to the half-life of carbon-14, indicates its potential use for dating ancient objects. The decay of radioactive substances follows an exponential model, and by studying the remaining atoms over time, the half-life provides a crucial parameter for dating applications.
The accuracy of this determination is demonstrated by fitting the decay equation to data points, ensuring reliability in age estimation. The similarity to the half-life of carbon-14, commonly used in archaeology, suggests that substance X could serve as a reliable tool for dating ancient artifacts and materials.