Answer: 0.3413
Explanation:
Given: an American household generates an average of 28 pounds of newspaper for garbage or recycling. Assume the standard deviation is 2 pounds.
Let
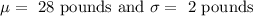 .
.
Let x be the random variable that denotes the amount of newspaper for garbage generated by each household each month.
If the data conforms to a normal distribution and a household is selected at random, the probability of its generating between 28 and 30 pounds per month is about
![P(28<x<30)=P((28-28)/(2)<(x-\mu)/(\sigma)<(30-28)/(2))\\\\=P(0<z<1)\ \ \ [\because\ z=(x-\mu)/(\sigma)]\\\\ =P(z<1)-P(z<0)\\\\=0.8413-0.5=0.3413](https://img.qammunity.org/2021/formulas/mathematics/college/nwrgtun0pxwmjaxvf9j557wvczx694r1rn.png)
Hence, the required probability is 0.3413.