Question

Raymond calculated the surface area of a cone that has a diameter measure of 8 meters and a slant height of 20.5 meters. Analyze Raymond’s work. Is he correct? If not, what was his mistake? Yes, he is correct. No; in step 1 he used the diameter measure instead of the radius. No; in step 2 he incorrectly evaluated the power to 64 instead of 16. No; in step 3 he added the surface area and lateral area incorrectly.

Answer 1

The correct answer on EDG-2020 is:

No; in step 1 he used the diameter measure instead of the radius.

Explanation:

Answer 2

No; in step 2 he incorrectly evaluated the power to 64 instead of 16

Explanation:

The question is not complete, the steps taken by Raymond are not listed, but I would show you the correct way of calculating the surface area and you determine from where Raymond made a mistake.

Answer:

A cone is a shape in which a set of lines connect the top point which is a common point to its circular base. The surface area of a cone is given by:

`A=\pi r(r+√(h^2+r^2) )=\pi r(r+l)=\pi r^2+\pi rl`

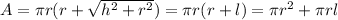
Where A is the surface area, r is the radius of the cone, h is the height of the cone and
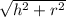`√(h^2+r^2)` is the length of the slant height of the cone.

Given that a cone has a diameter measure of 8 meters and a slant height of 20.5 meters. Therefore:

radius (r) = diameter/2 = 8 / 2 = 4 m

Slant height (l) = 20.5 m

The surface area is:

`A=\pi r^2+\pi rl\\Substituting \ values:\\A=\pi *4^2+\pi *4*20.5\\=\pi *16+\pi *82\\=98\pi \ m^2\\=307.9\ m^2`

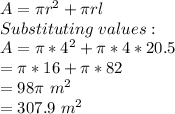
The power in step 2 is 16 not 64