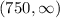Question

Profit Function for Producing Thermometers The Mexican subsidiary of ThermoMaster manufactures an indoor-outdoor thermometer. Management estimates that the profit (in dollars) realizable by the company for the manufacture and sale of x units of thermometers each week is represented by the function below, where x ≥ 0. 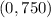Find the interval where the profit function P is increasing and the interval where P is decreasing. (Enter your answer using interval notation.) P(x) = −0.004x2 + 6x − 5,000 Increasing: Decreasing:

Answer 1

Increasing:
`(0, 750)`

Decreasing:
`(750, \infty)`

Explanation:

Critical points:

The critical points of a function f(x) are the values of x for which:

`f'(x) = 0`

For any value of x, if f'(x) > 0, the function is increasing. Otherwise, if f'(x) < 0, the function is decreasing.

The critical points help us find these intervals.

In this question:

`P(x) = -0.004x^(2) + 6x - 5000`

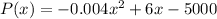
So

`P'(x) = -0.008x + 6`

Critical point:

`P'(x) = 0`

`-0.008x + 6 = 0`

`0.008x = 6`

`x = (6)/(0.008)`

`x = 750`

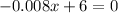
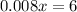
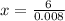
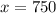
We have two intervals:

(0, 750) and
`(750, \infty)`

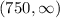
(0, 750)

Will find P'(x) when x = 1

`P'(x) = -0.008x + 6 = -0.008*1 + 6 = 5.992`

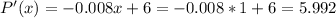
Positive, so increasing.

Interval
`(750, \infty)`

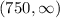
Will find P'(x) when x = 800

`P'(x) = -0.008x + 6 = -0.008*800 + 6 = -0.4`

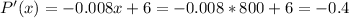
Negative, then decreasing.

Answer:

Increasing:
`(0, 750)`

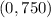
Decreasing:
`(750, \infty)`