Question

EXAMPLE 3 If f(x, y) = 4xy2 7x2 + y4 , does lim (x, y)→(0, 0) f(x, y) exist? SOLUTION Let's try to save some time by letting (x, y) → (0, 0) along any nonvertical line through the origin. Then y = mx, where m is the slope, and f(x, y) = f(x, mx) = 4x 2 7x2 + (mx)4 = 7x2 + m4x4 = 7 + m4x2 .

Answer 1

Limit of the function exists.

Explanation:

Given the function f(x,y) =
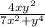`(4xy^(2) )/(7x^(2) + y^(4) )`, we are to show that lim (x, y)→(0, 0) f(x, y) exist. To show that, the following steps must be followed.

`\lim_((x,y) \to (0,0)) (4xy^(2) )/(7x^(2) + y^(4) )\\`

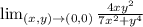
substituting the limit x = 0 and y = 0 into the function we have;

`(4(0)^(2) )/(7(0)^(2) + (0)^(4) )\\= (0)/(0) (indeterminate)`

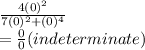
Since we got an indeterminate function, we will then substitute y = mx into the function as shown;

`\lim_((x,mx) \to (0,0)) (4x(mx)^(2) )/(7x^(2) + (mx)^(4) )\\\lim_((x,mx) \to (0,0)) (4m^(2) x^(3) )/(7x^(2) + m^(4)x^(4) )\\\\\lim_((x,mx) \to (0,0)) (4m^(2) x^(3) )/(x^(2)(7 + m^(4) x^(2)) )\\\lim_((x,mx) \to (0,0)) (4m^(2)x )/(7 + m^(4) x^(2) )`

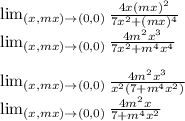
Substituting x = 0 , the limit of the function becomes;

`(4m^(2)(0) )/(7 + m^(4) (0)^(2) )\\= (0)/(7)\\ = 0`

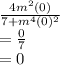
Since the limit of the function gives a finite value of 0 (the limit tends to 0). This shows that the limit exists.