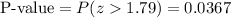Question

The mayor of a town has proposed a plan for the construction of an adjoining community. A political study took a sample of 900 voters in the town and found that 45% of the residents favored construction. Using the data, a political strategist wants to test the claim that the percentage of residents who favor construction is over 42%. Determine the P-value of the test statistic. Round your answer to four decimal places.

Answer 1

P-value = 0.0367

Explanation:

This is a hypothesis test for a proportion.

The claim is that the percentage of residents who favor construction is significantly over 42%.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.42\\\\H_a:\pi>0.42`

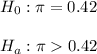
The sample has a size n=900.

The sample proportion is p=0.45.

The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.42*0.58)/(900)}\\\\\\ \sigma_p=√(0.000271)=0.016`

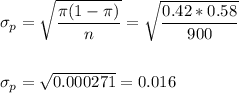
Then, we can calculate the z-statistic as:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.45-0.42-0.5/900)/(0.016)=(0.029)/(0.016)=1.79`

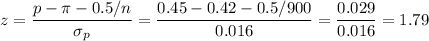
This test is a right-tailed test, so the P-value for this test is calculated as:

`\text{P-value}=P(z>1.79)=0.0367`