Question

Find the volume of a cone with a diameter of 18 meters and a height of 20 meters

Answer 1

The volume of the cone is approximately 1,896.48 cubic meters.

Step-by-step explanation:

The volume of a cone can be calculated using the formula,
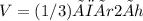`V = (1/3) × π × r2 × h` where r is the radius and h is the height of the cone.

In this case, the diameter of the cone is given as 18 meters, which means the radius (r) will be half of that, i.e. 9 meters. The height (h) is given as 20 meters.

Substituting these values into the formula, we get
`V = (1/3) × π × 92 × 20.`

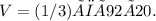
Using the value of π as 3.142, the volume of the cone is approximately 1,896.48 cubic meters.

Answer 2

`\huge \sf \color{pink}{A} \color{green}{N} \color{red}{S} \color{blue}{W} \color{orange}{E} \color{grey}{R}`

`\large \underline{ \boxed{ \sf{✰ \: Important \: points }}}`

`\pink{➢}` Diameter of cone = 18m

`\pink{➢}`Height of cone = 20m

`\pink{➢}`A surface of revolution formed by rotating a segment of a line around another line that intersects the first line.

`\pink{➢}`Cone is basically formed by circular base

`\underline{ \boxed{ \sf{➫\: Volume\:of\:cone = (1)/(3) {r}^(2) \pi \: h}}}`

`\underline{ \boxed{ \sf{ ➪ \: r = radius}}} \\\underline{ \boxed{ \sf{ ➪ \: h = height}}}`

`\pink{➢}` We know that radius is half of diameter

`\sf \:➩ r = (18)/(2) \\ \sf \: ➩r = \cancel (18)/(2) \\ \sf \: ➩r = 9 \: \: \:`

`\pink{➢}`Hence radius of cone in data given is 9m

➢ Let's substitute values according to formula

`\sf \: → (1)/(3) * {(9)}^(2)* 3.14 *20 \\ \sf→ (1)/(3) * 81 * 3.14 * 20 \\ \sf \: → (1)/( \cancel3) * \cancel{81} * 3.14 * 20 \\ \sf→27 * 3.14 * 20 \\ \sf \: →1695.6m`

`\pink{➢}` Hence volume of cone =1695.6m

Hope it helps !