Question

Janet wants to estimate the percentage of people who have been required to take a drug test for work. She surveys 250 individuals and finds that 175 have taken a drug test for work. Identify the values needed to calculate a confidence interval at the 98% confidence level. Then find the confidence interval.

Answer 1

98% of confidence interval for the true population

(0.6326 , 0.7674)

Explanation:

Step(i):-

Given sample size 'n' = 250

She surveys 250 individuals and finds that 175 have taken a drug test for work.

sample proportion

`p = (x)/(n) = (175)/(250) =0.7`

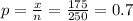
level of significance ∝ = 0.05

98% of confidence interval for the true population is determined by

`(p^(-) - Z_(0.02) \sqrt{(p(1-p))/(n) } ,p +Z_(0.02) \sqrt{(p(1-p))/(n) } )`

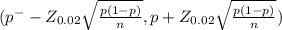
Z₀.₀₂ = 2.326

Step(ii):-

98% of confidence interval for true population is determined by

`(0.7 - 2.326\sqrt{(0.7(1-0.7))/(250) } ,0.7 + 2.326 \sqrt{(0.7(1-0.7))/(250) } )`

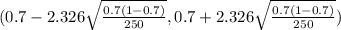
( 0.7 - 0.0674 , 0.7 + 0.0674)

(0.6326 , 0.7674)

Conclusion:-

98% of confidence interval for the true population is determined by

(0.6326 , 0.7674)