Question

Suppose 180 randomly selected people are surveyed to determine whether or not they plan on reelecting the current president. Of the 180 surveyed, 36 reported they will not vote to reelect the current president. What is the correct interpretation of the 99% confidence interval? Select the correct answer below: We estimate with 99% confidence that the sample proportion of people who will not vote to reelect the current president is between 0.123 and 0.277. We estimate with 99% confidence that the true population proportion of people who will not vote to reelect the current president is between 0.123 and 0.277. We estimate that 99% of the time a survey is taken, the proportion of people who will not vote to reelect the current president is between 0.123 and 0.277.

Answer 1

b)

we estimate with 99% confidence that the true population proportion of people who will not vote to reelect the current president

(0.1236 , 0.2764)

Explanation:

Step(i):-

Given sample size 'n' = 180

Given data the 180 surveyed, 36 reported they will not vote to reelect the current president.

Sample proportion

`p = (x)/(n) = (36)/(180) = 0.2`

level of significance ∝=0.99 or 0.01

The 99% confidence for the true population proportion is determined by

`(p^(-) - Z_(0.01) \sqrt{(p(1-p))/(n) } , p^(-) + Z_(0.01) \sqrt{(p^(-) (1-p^(-) ))/(n) } )`

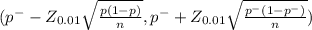
Z₀.₀₁ = 2.576

The 99% confidence for the true population proportion is determined by

`(0.2 - 2.576 \sqrt{(0.2(1-0.2))/(180) } , 0.2+ 2.576 \sqrt{(0.2 (1-0.2 ))/(180) } )`

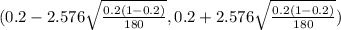
(0.2 - 0.0764 , 0.2 +0.0764)

(0.1236 , 0.2764)

Conclusion:-

The 99% confidence for the true population proportion of people who will not vote to reelect the current president

(0.1236 , 0.2764)