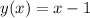Question

Find all the points at which the direction of fastest change of the function f(x, y) = x2 + y2 − 4x − 2y is i + j.

Answer 1

All the points that lie on the line:

`y(x)=x-1`

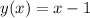
Explanation:

In order to find the maximum rate of change, we need to find the gradient of the function. The gradient of a function of two variables is defined to be:

`\\abla f =(\partial f)/(\partial x) i + (\partial f)/(\partial y) j`

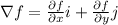
So:

`(\partial f)/(\partial x) = 2x-4=2(x-2)\\\\(\partial f)/(\partial y) = 2y-2=2(y-1)`

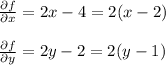
Hence:

`\\abla f(x,y)=2(x-2)i+2(y-1)j`

Since we need to find all the points at which the direction of fastest change of the function
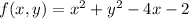`f(x,y)=x^(2) +y^(2) -4x-2` is
`i+j`. Then:

`2(x-2)i+2(y-1)=ai+aj\\\\a>0`

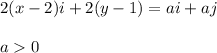
Therefore:

`2(x-2)=2(y-1)\\\\Solving\hspace{3}for\hspace{3}y\\\\y=x-1`

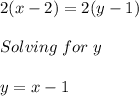
So, we can conclude, that all the points where the direction of fastest change of
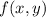`f(x,y)` lie on the line:

`y(x)=x-1`