Question

a silver coin is dropped from the top of a building that is 64 feet tall. the position function of the coin at time t seconds is represented by

Answer 1

Question:

A silver coin is dropped from the top of a building that is 64 feet tall. the position function of the coin at time t seconds is represented by

s(t) = -16t² + v₀t + s₀

Determine the position and velocity functions for the coin.

Answer:

position function: s(t) = (-16t² + 64) ft

velocity function: v(t) = (-32t) ft/s

Explanation:

Given position equation;

s(t) = -16t² + v₀t + s₀ ---------(i)

v₀ and s₀ are the initial values of the velocity and position of the coin respectively.

(a) Since the coin is dropped, the initial velocity, v₀, of the coin is 0 at t = 0. i.e

v₀ = 0.

Also since the drop is from the top of a building that is 64 feet tall, this implies that the initial position, s₀, of the coin is 64 ft at t=0. i.e

s₀ = 64ft

Substitute the values of v₀ = 0 and s₀ = 64 into equation (i) as follows;

s(t) = -16t² + (0)t + 64

s(t) = -16t² + 64

Therefore, the position function of the coin is;

s(t) = (-16t² + 64) ft

(b) To get the velocity function, v(t), the position function, s(t), calculated above is differentiated with respect to t as follows;

v(t) =
`(ds(t))/(dt)`

v(t) =
`(d(-16t^2 + 64))/(dt)`

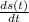
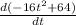
v(t) = -32t + 0

v(t) = -32t

Therefore, the velocity function of the coin is;

v(t) = (-32t) ft/s