Question

It is known that the gravitational force of attraction between two alpha particles is much weaker than the electrical repulsion. For two alpha particles at a distance d apart, calculate the ratio of the size of the gravitational attraction to that of the electrical repulsion. Specifically, find the magnitude of Gravitational/Electrical.

Answer 1

The ratio of gravitational force to electrical force is 3.19 x 10^-36

Step-by-step explanation:

mass of an alpha particle = 6.64 x
`10^(-27)` kg

charge on an alpha particle = +2e = +2(1.6 x
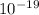`10^(-19)` C) = 3.2 x
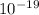`10^(-19)` C

distance between particles = d

For gravitational attraction:

The force of gravitational attraction F =
`(Gm^(2) )/(r^(2) )`

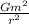
where G = gravitational constant = 6.67 x
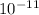`10^(-11)` m^3 kg^-1 s^-2

r = the distance between the particles = d

m = the mass of each particle

therefore, gravitational force =
`(6.67*10^(-11)*(6.64*10^(-27) )^(2) )/(d^(2) )` =
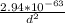`(2.94*10^(-63) )/(d^(2) )` Newton

For electrical repulsion:

Electrical force between the particles =
`(-kQ^(2) )/(r^(2) )`

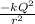
where k is the Coulomb's constant = 9.0 x
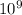`10^(9)` N•m^2/C^2

r = distance between the particles = d

Q = charge on each particle

therefore, electrical force =
`(-9*10^(9)*(3.2*10^(-19) )^(2) )/(d^(2) )` =
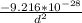`(-9.216*10^(-28) )/(d^(2) )` Newton

the negative sign implies that there is a repulsion on the particles due to their like charges.

Ratio of the magnitude of gravitation to electrical force =
`(2.94*10^(-63) )/(9.216*10^(-28) )`

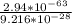
==> 3.19 x 10^-36