Question

A coil has resistance of 20 W and inductance of 0.35 H. Compute its reactance and its impedance to an alternating current of 25 cycles/s.

Answer 1

The reactance of the coil at 25 Hz is approximately 55 ohms, and the total impedance is approximately 58.9 ohms.

Step-by-step explanation:

To calculate the reactance (XL) of the coil due to its inductance (L) when exposed to an alternating current (AC) of frequency (f), we use the formula XL = 2πfL. In this case, the inductance is 0.35 H, and the frequency is 25 cycles/s or Hz. Plugging in the values, we get XL = 2π(25Hz)(0.35H) = 55 ohms approximately.

To find the impedance (Z) of the coil, which is the total opposition a circuit presents to the flow of alternating current, we combine the coil's resistance (R) and inductive reactance (XL) in a square root of the sum of squares fashion since they are orthogonal components: Z = √(R2 + XL2). Given that the resistance R is 20 ohms and we have found XL to be approximately 55 ohms, the impedance is Z = √(202 + 552) which calculates to roughly 58.9 ohms.

Answer 2

• Reactance of the coil is 55 W

• Impedance of the coil is 59 W

Step-by-step explanation:

Given;

Resistance of the coil, R = 20 W

Inductance of the coil, L = 0.35 H

Frequency of the alternating current, F = 25 cycle/s

Reactance of the coil is calculated as;

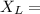`X_L=` 2πFL

Substitute in the given values and calculate the reactance
`(X_L)`

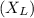
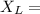`X_L =` 2π(25)(0.35)

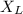`X_L` = 55 W

Impedance of the coil is calculated as;

`Z = √(R^2 + X_L^2) \\\\Z = √(20^2 + 55^2) \\\\Z = 59 \ W`

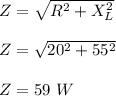
Therefore, the reactance of the coil is 55 W and Impedance of the coil is 59 W