Question

Suppose that a baseball player has been a .250 hitter for his career, which means that his probability of a hit (success) has been 0.250. Then during one winter the player genuinely improves to the point that his probability of success improves to 0.333. You will investigate how likely the player is, in a sample of at-bats, to convince the manager that he has improve

Answer 1

To convince the manager that he has improved, we need to take a sample and test against the null hypothesis that states that the proportion of success of this player is not significantly higher than 0.250.

If we have a sample of size n=20 with sample proportion 0.333, at a significance level of 0.05, there is not enough evidence to support the claim that the proportion of success is greater than 0.250.

Explanation:

In this case, to demostrate that the baseball player has improved his probability of success over 0.250, we need to know the sample size of that winter (that gives p=0.333) and then perform a hypothesis test on the proportion of at-bats.

Lets assume the sample is n=20, and the sample proportion is p=0.333.

The claim is that the proportion of success is greater than 0.250.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.25\\\\H_a:\pi>0.25`

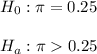
The significance level is 0.05.

The sample has a size n=20.

The sample proportion is p=0.333.

The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.25*0.75)/(20)}\\\\\\ \sigma_p=√(0.009375)=0.097`

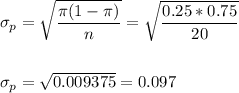
Then, we can calculate the z-statistic as:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.333-0.25-0.5/20)/(0.097)=(0.058)/(0.097)=0.599`

This test is a right-tailed test, so the P-value for this test is calculated as:

`\text{P-value}=P(z>0.599)=0.275`

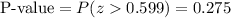
As the P-value (0.275) is greater than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

At a significance level of 0.05, there is not enough evidence to support the claim that the proportion of success is greater than 0.250.